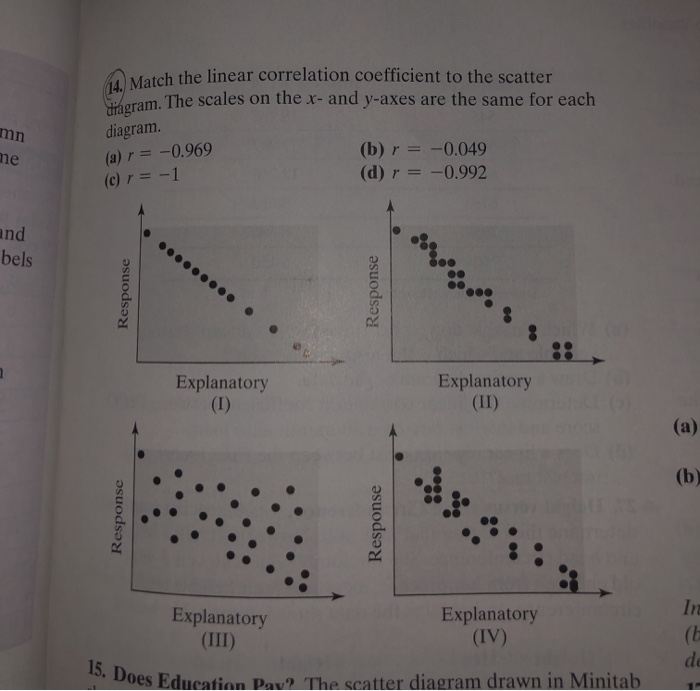
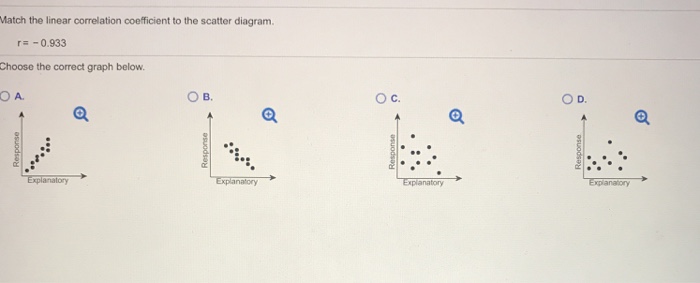
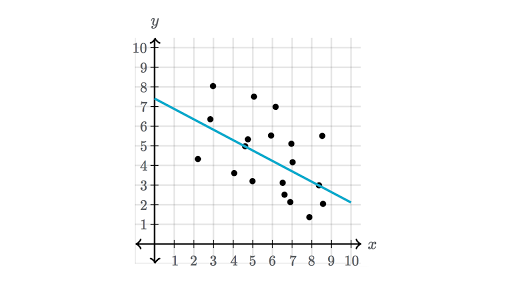
42 match the linear correlation coefficient to the scatter diagram.
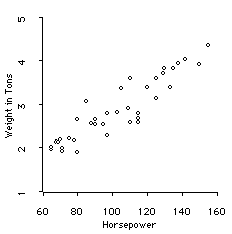
Correlation coefficients are used to measure the strength of the linear relationship between two variables. A correlation coefficient greater than zero indicates a positive relationship while a ... A scatterplot is a type of data display that shows the relationship between two numerical variables. Each member of the dataset gets plotted as a point whose coordinates relates to its values for the two variables. For example, here is a scatterplot that shows the shoe sizes and quiz scores for students in a class: Created with Raphaël.
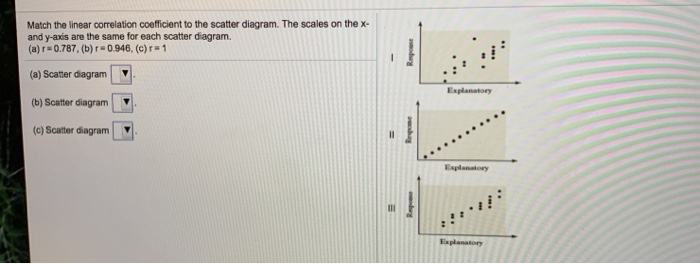
Match the linear correlation coefficient to the scatterdiagram. The scales on the x and yaxis are the same foreach scatter diagram.(a) r = − 0.049, (b) r =...
Match the linear correlation coefficient to the scatter diagram.
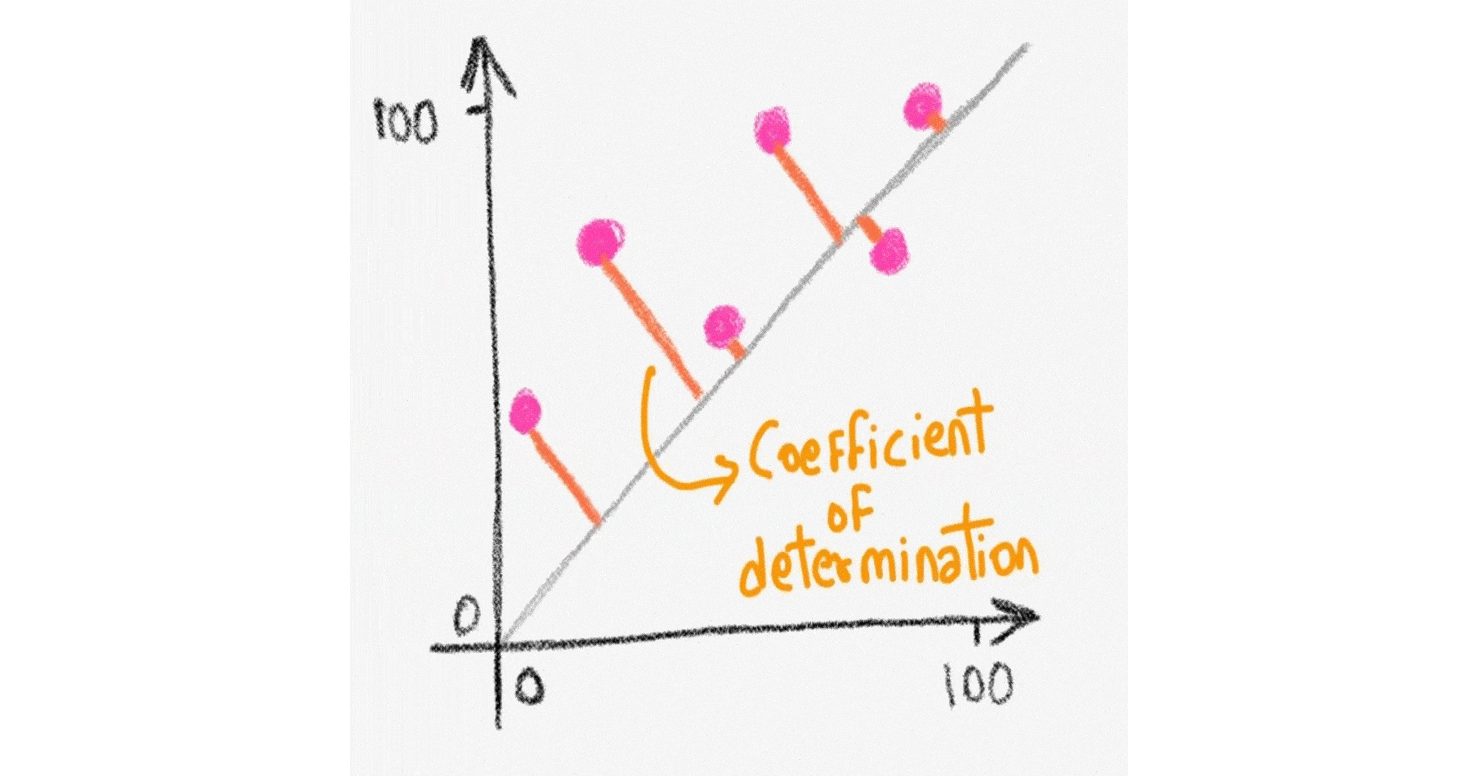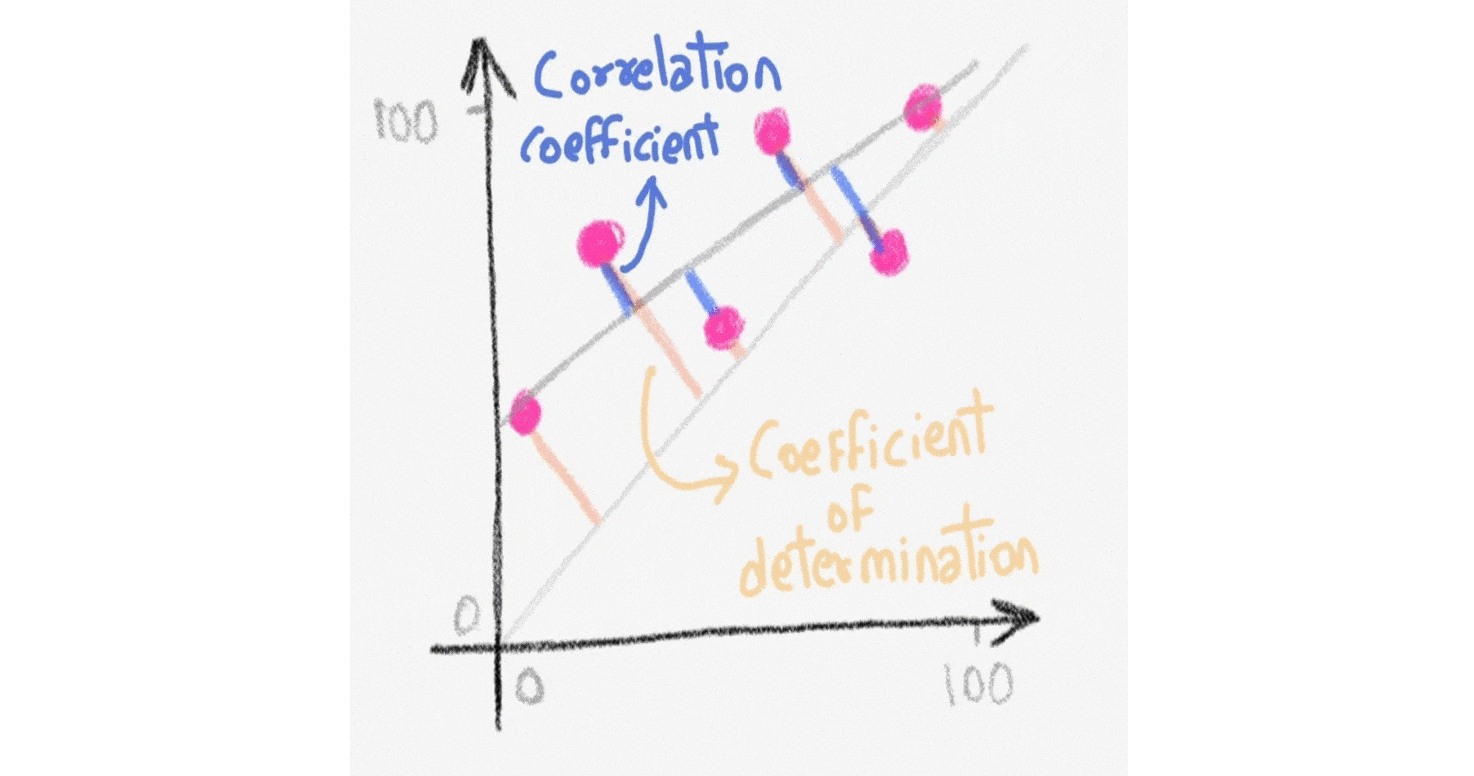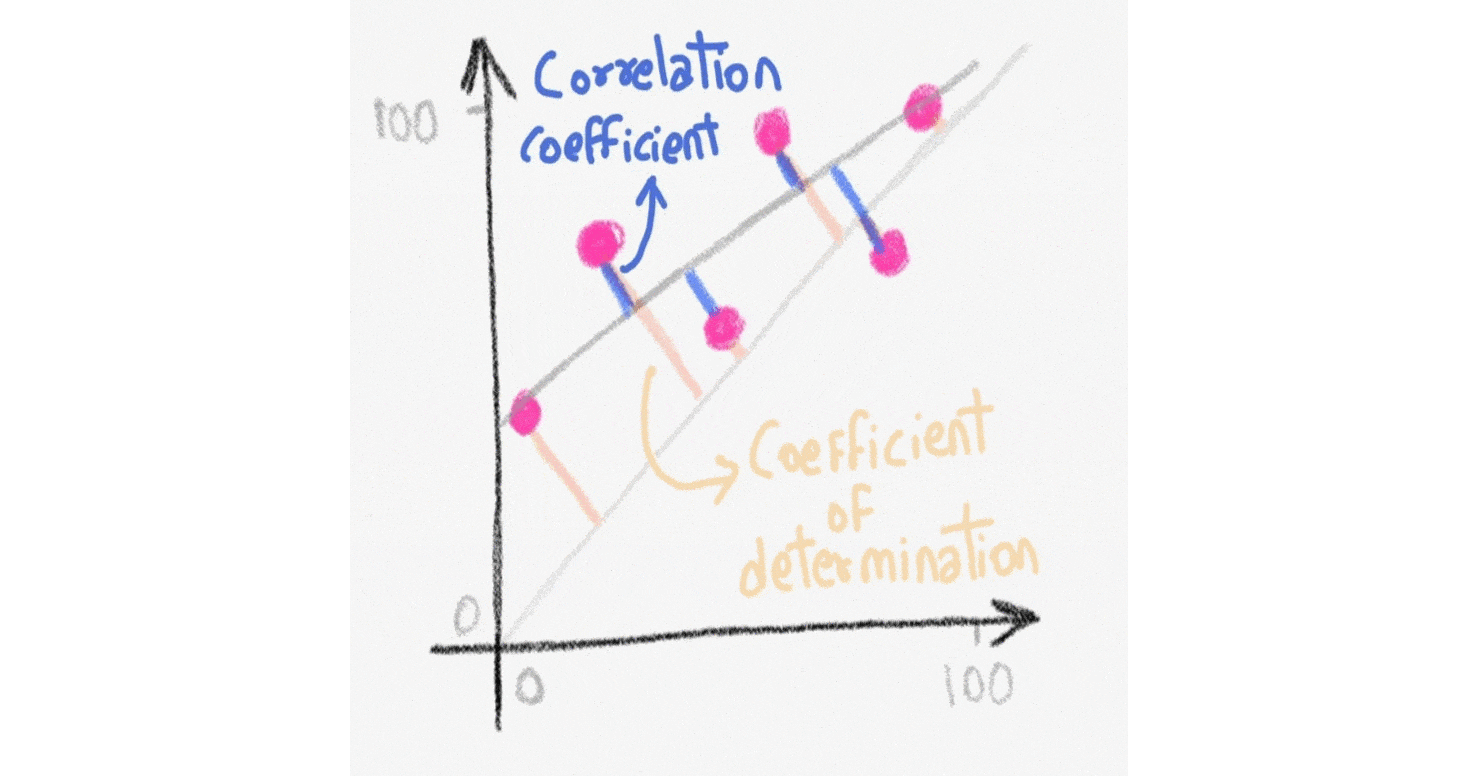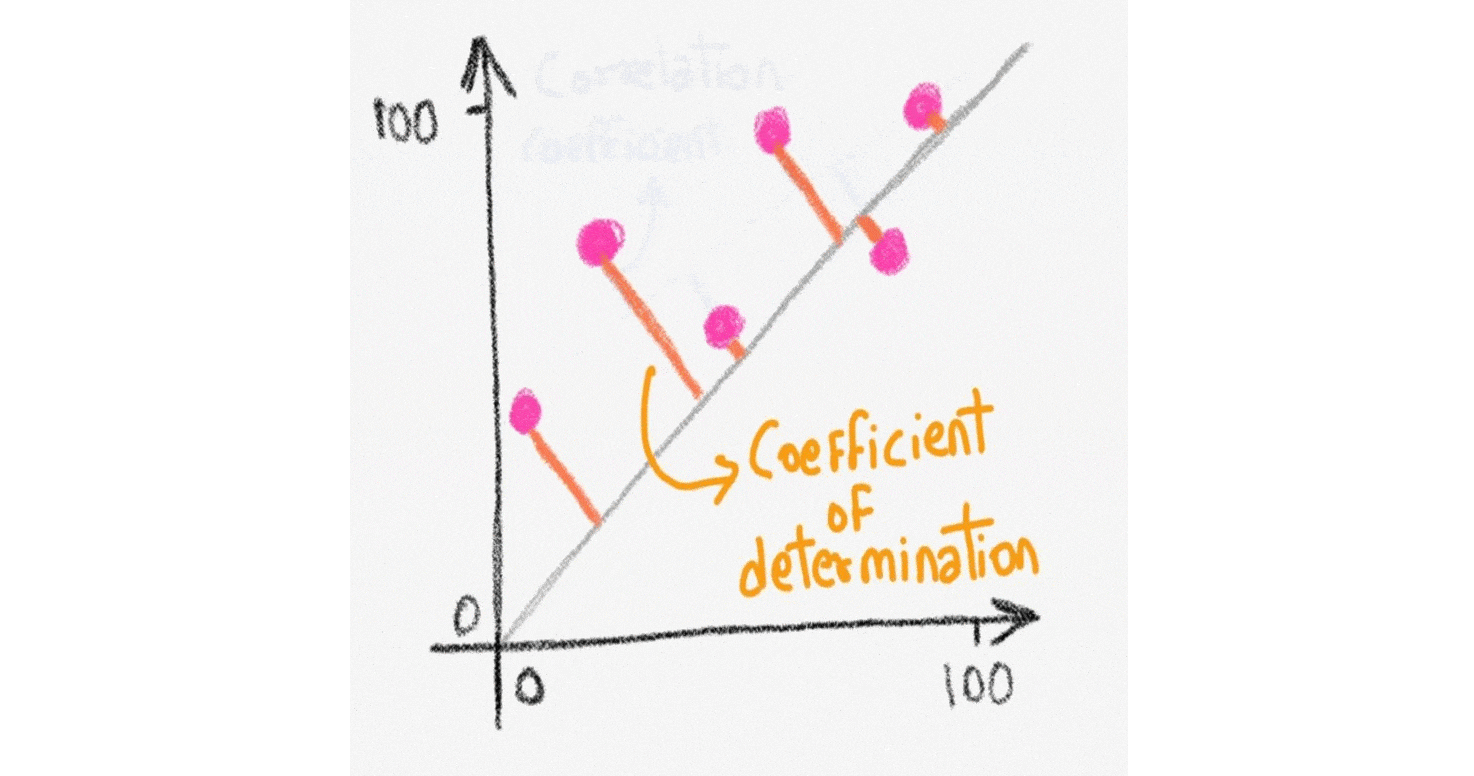
Coefficient of Determination: Unless the correlation coefficient V is exactly or very nearly +1, -1 or 0, its meaning is a little inexact. For example, if the correlation coefficient for two variables is + 0.8, this would tell us that the variables are positively correlated, but the correlation is not perfect. It does not really tell us much else. Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram. (a) r = -1 , (b) r = -0.049 , (c) r = -0.992 Use this utility to create box plots, aka box and whiskers diagrams from a set of observations. Linear regression. The simple linear regression calculator derives and plots the line of best fit from a set of bivariate data. Sample correlation coefficient. Calculate the correlation coefficient. Scatter-plot generator. Make scatter diagrams ...
Match the linear correlation coefficient to the scatter diagram.. The Takeaways. Scatter plots are a method of mapping one variable compared to another. This map allows you to see the relationship that exists between the two variables. The relationship can vary as positive, negative, or zero. The relationship is numerically represented by the correlation coefficient and the coefficient of determination. 1) The strength of the relationship given by the correlation coefficient. 2) The direction of the relationship, which can be positive or negative based on the sign of the correlation coefficient. 3) The shape of the relationship, which must always be linear to computer a Pearson correlation coefficient. The correlation coefficient, r, tells how closely the scatter diagram points are to being on a line. If the correlation coefficient is positive, the line slopes upward. If the correlation coefficient is negative, the line slopes downward. All values of the correlation coefficient are between -1 and 1, inclusive. Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram (a)r= - 1.1 answer · Top answer: Using the given scatter diagram, a) Scatter diagram I That is r-0.969 Explanatory aoday b) Scatter diagram III That is r=-1 Esplansory c) Scatter diagram ...
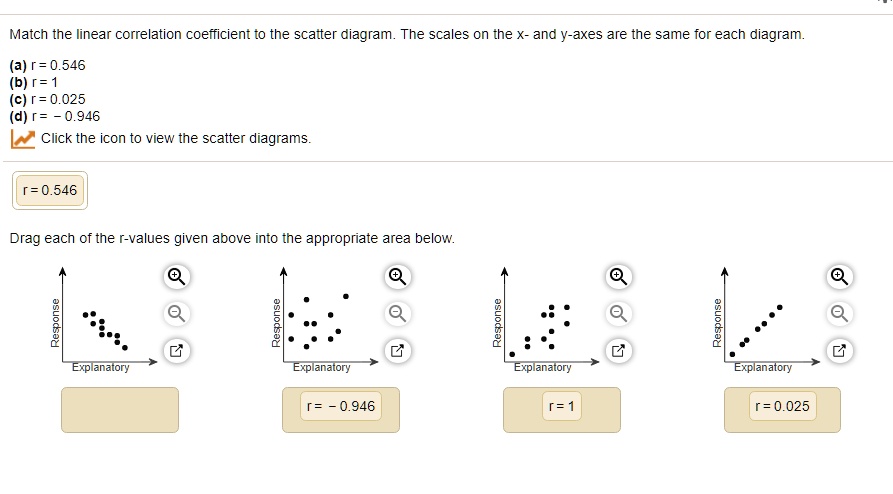
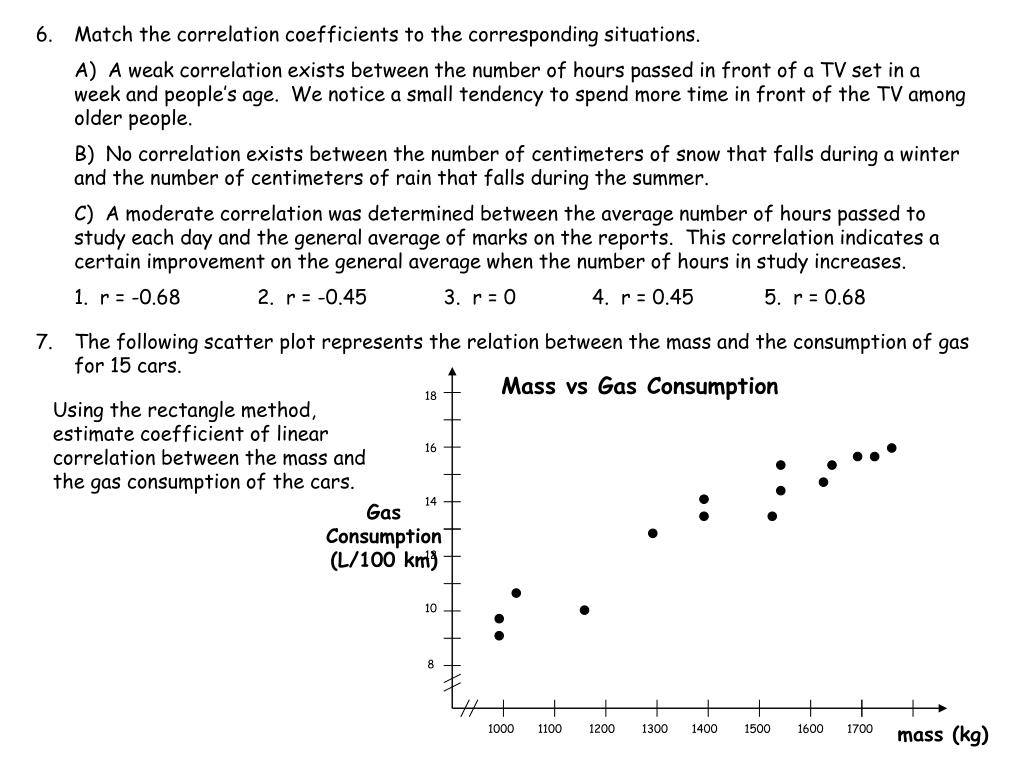
Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axes are the same for each diagram. (a) r = 0.025 (b) r= -0.992 (c) r = 0.523 (d) r= 1 Click the icon to view the scatter diagrams. r= 0.025 r= 0.523 r= -0.992 r=1 Drag each of the r-values given above into the appropriate area below. Response Response ... Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axes are the same for each diagram. (a) r= -0.546 (b) r= -0.992 (c) r= -1 (d) r= -0.038 Click the icon to view the scatter diagrams. r= -0.038 r= -0.992 r= -1 r= -0.546 Drag each of the r-values given above into the appropriate area below. Ø Ø 3 ... Basic Concepts. To better visualize the association between two data sets {x 1, …, x n} and {y 1, …, y n} we can employ a chart called a scatter diagram (also called a scatter plot).This is done in Excel by highlighting the data in the two data sets and selecting Insert > Charts|Scatter.. Figure 1 illustrates the relationship between a scatter diagram and the correlation coefficient (or ... Transcribed image text: Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axes are the same for each gram.
Correlation is defined as the statistical association between two variables. A correlation exists between two variables when one of them is related to the other in some way. A scatterplot is the best place to start. A scatterplot (or scatter diagram) is a graph of the paired (x, y) sample data with a horizontal x-axis and a vertical y-axis. The Correlation Coefficient (r) The sample correlation coefficient (r) is a measure of the closeness of association of the points in a scatter plot to a linear regression line based on those points, as in the example above for accumulated saving over time. Possible values of the correlation coefficient range from -1 to +1, with -1 indicating a ... The scales on the x and y axes. Matching correlation coefficients to scatter plots. The scales on the x and y axis are the same for each scatter diagram. A r 0049 b r 1 c r 0810. D r 0992. Match the linear correlation coefficient to the scatter diagram. Find the linear correlation coefficient r if given the following x and y values. A r 0969 iii. Match the linear correlation coefficient to the scatter diagram.r = - 0.049 Follow me at https://web.facebook.com/statisticsmcq/
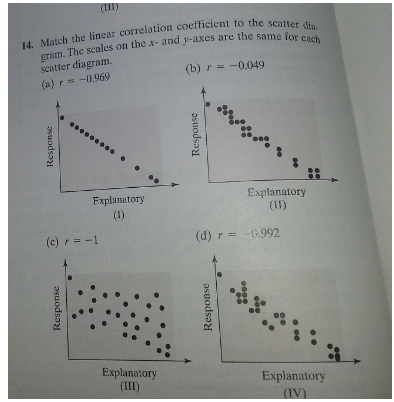
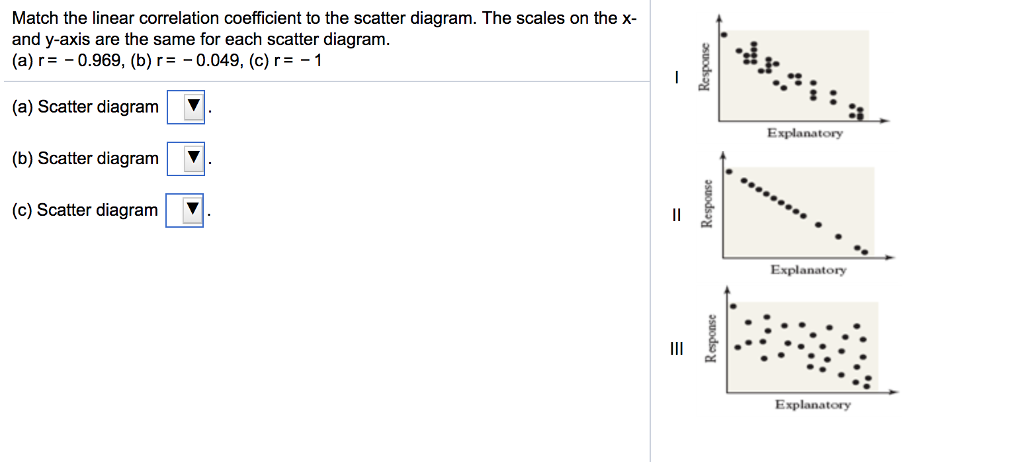
Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axes are The same for each diagram. (a) r = −0.969 (b) r = −0.049 (c) r = −1 (d) r = −0.992 Answer: I : (c) r = -1 II : (a) r = -0.969 III : (b) r = -0.049 IV : (d) r = -0.992
we're working with correlation coefficients and scattered diagram. So were given four correlation coefficients that you can see up top here. And we'd like to match these with the scatter diagram that fits it. So let's start with our first diagram um in the upper left corner and this one looks to be a fairly straight line. So if we were to draw a trend line through it it would look something ...
Match the linear correlation coefï¬cient to the scatter diagrams. The scales on the x- and y-axes are the same for each diagram.(a) r = 0.787(b) r = 0.523(c) r = 0.053(d) r = 0.946 View Answer Match the following scatter plots with the correlation values.1.
IXL's SmartScore is a dynamic measure of progress towards mastery, rather than a percentage grade. It tracks your skill level as you tackle progressively more difficult questions. Consistently answer questions correctly to reach excellence (90), or conquer the Challenge Zone to achieve mastery (100)! Learn more.
The linear correlation coefficient is always between -1 and 1. If r = +1, there is a perfect positive linear relation between the two variables. If r = -1, there is a perfect negative linear relation between the two variables. The closer r is to +1, the stronger is the evidence of positive association between the two variables.
Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram. (a) r= - 0.969, (b) r= - 0.049, (c) r= -1 (a) Scatter diagram Explanatory (b) Scatter diagram (c) Scatter diagram Explanatory II Explanatory
Improve your math knowledge with free questions in "Match correlation coefficients to scatter plots" and thousands of other math skills.
Yes, the correlation coefficient measures two things, form and direction. If you have two lines that are both positive and perfectly linear, then they would both have the same correlation coefficient. The only way the slope of the regression line relates to the correlation coefficient is the direction.
You just studied 6 terms! Now up your study game with Learn mode. Look at a scatter plot and estimate a correlation coefficient value and interpret as a strong positive, strong negative, etc...
Transcribed image text: Match the linear correlation coefficient to the scatter diagram. The scales on thex and y-axis are the same for each scatter diagram ...
The linear correlation coefficient has the following properties, illustrated in Figure 10.4 "Linear Correlation Coefficient ": . The value of r lies between −1 and 1, inclusive.; The sign of r indicates the direction of the linear relationship between x and y: . If r < 0 then y tends to decrease as x is increased.; If r > 0 then y tends to increase as x is increased.
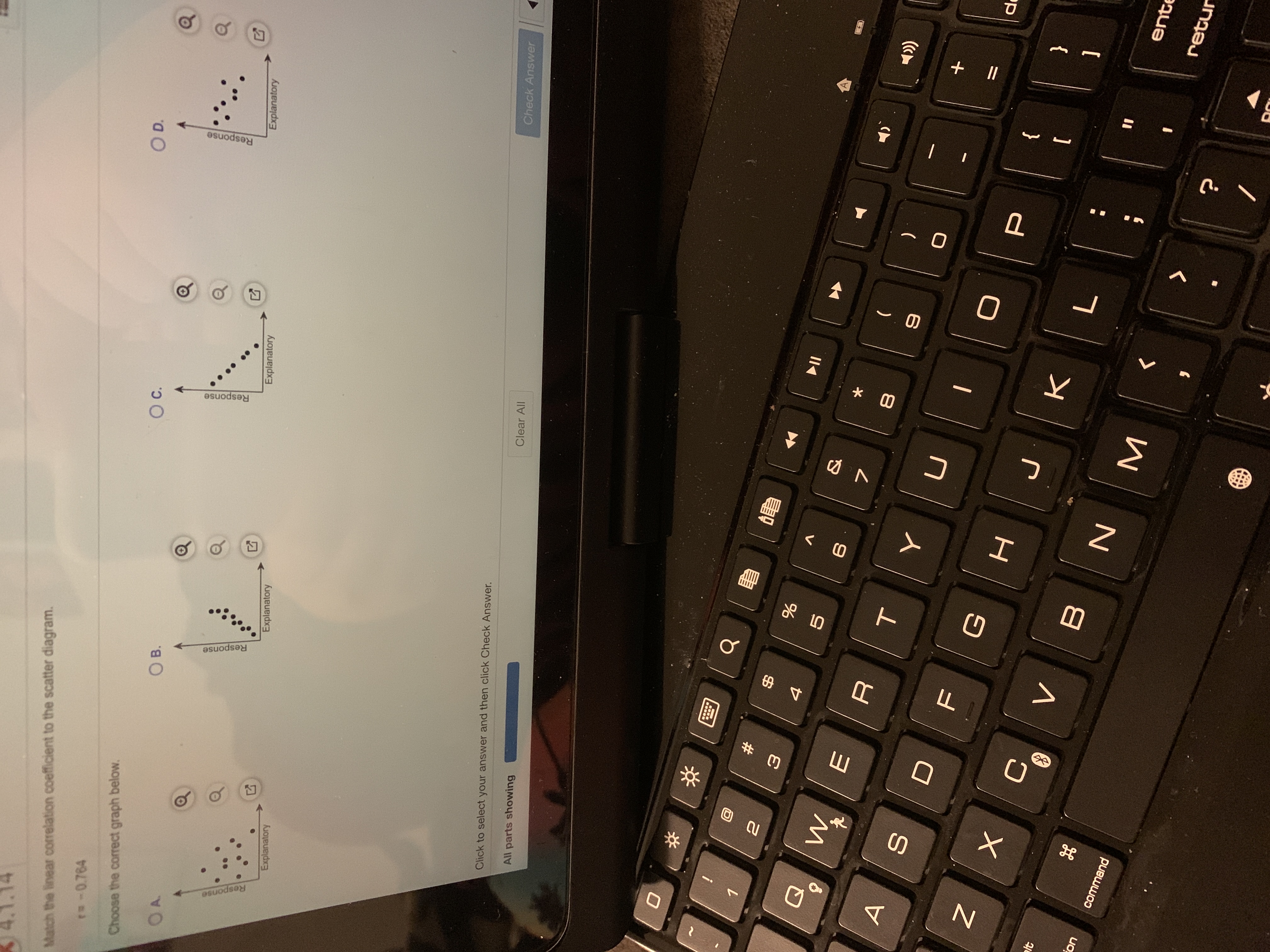
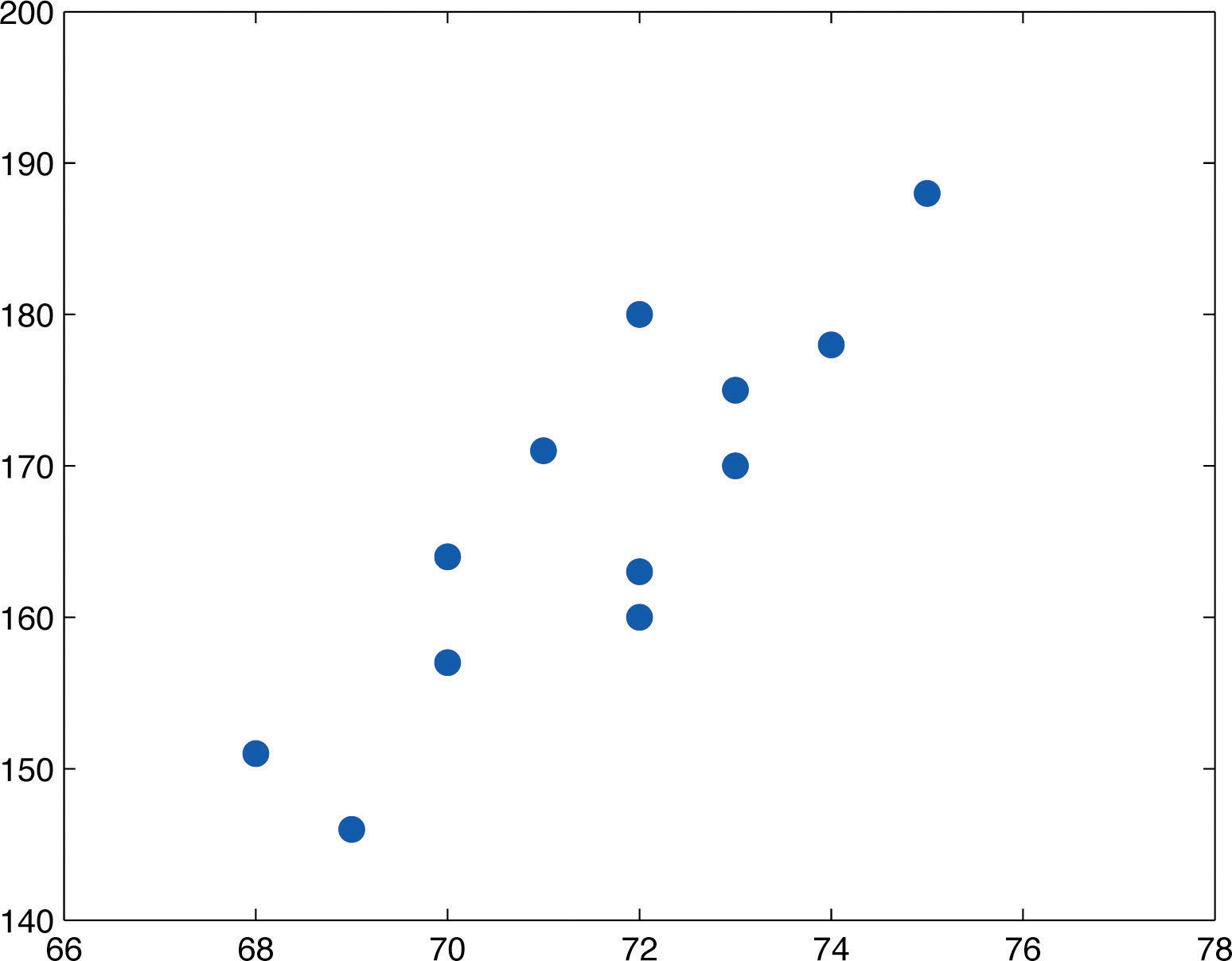
Question: Match the linear correlation coefficient to the scatter diagram. r= -0.764 Choose the correct graph below. This problem has been solved! See the ...
Statistics Q&A Library Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram. (a) r= 0.946, (b) r= 0.523, (c) r= 1 (a) Scatter diagram (b) Scatter diagram Explanatory (c) Scatter diagram ..... Explanatory II Explanatory
The Correlation Coefficient • The strength of a linear relationship is measured by the correlation coefficient • The sample correlation coefficient is given the symbol “r” • The population correlation coefficient has the symbol “ρρρ”. Chapter 5 # 10 Interpreting r • The sign of the correlation coefficient tells us the
Correlation refers to a process for establishing the relationships between two variables. You learned a way to get a general idea about whether or not two variables are related, is to plot them on a "scatter plot". . While there are many measures of association for variables which are measured at the ordinal or higher level of measurement, correlation is the most commonly used approach.
Transcribed image text: Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter ...
Use this utility to create box plots, aka box and whiskers diagrams from a set of observations. Linear regression. The simple linear regression calculator derives and plots the line of best fit from a set of bivariate data. Sample correlation coefficient. Calculate the correlation coefficient. Scatter-plot generator. Make scatter diagrams ...
Match the linear correlation coefficient to the scatter diagram. The scales on the x- and y-axis are the same for each scatter diagram. (a) r = -1 , (b) r = -0.049 , (c) r = -0.992
Coefficient of Determination: Unless the correlation coefficient V is exactly or very nearly +1, -1 or 0, its meaning is a little inexact. For example, if the correlation coefficient for two variables is + 0.8, this would tell us that the variables are positively correlated, but the correlation is not perfect. It does not really tell us much else.



.png)


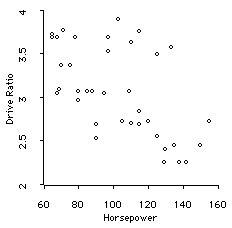











0 Response to "42 match the linear correlation coefficient to the scatter diagram."
Post a Comment